Question

Cullen (1994) took a sample of the 580 children served by an Auckland family practice to estimate the proportion of interest. What sample size in an SRS (without replacement) would he necessary to estimate the proportion with 95% confidence and margin of error 0.10? Cullen actually took an SRS with replacement of size 120, of whom 27 were not overdue for vaccination. Give a 95% CI for the proportion of children not overdue for vaccination

Answer 1

(1) The sample size required is 97.

(2) The 95% confidence interval for the proportion of children not overdue for vaccination is (0.15, 0.30).

Explanation:

(1)

Let the proportion be, p = 0.50.

The margin of error formula is:

`MOE=z* \sqrt{(p(1-p))/(n)}`

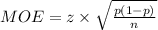
The critical value of z for 95% confidence level is,

z = 1.96 (Use the standard normal table for z values)

Compute sample size n as follows:

`n=((z)/(MOE))^(2)* p(1-p)\\=((1.96)/(0.10) )^(2)* 0.50* (1-0.50)\\=96.04\\\approx97`

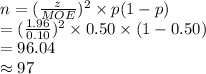
Thus, the sample size required is 97.

(2)

The confidence interval for population proportion is:

`\hat p\pm z\sqrt{(\hat p(1-\hat p))/(n) }`

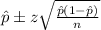
The sample size is, n = 120.

The number of children who were not overdue for vaccination, X = 27.

The sample proportion is:

`\hat p=(X)/(n)= (27)/(120)= 0.225`

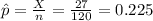
The critical value of z for 95% confidence level is z = 1.96.

The 95% confidence interval is:

`\hat p\pm z\sqrt{(\hat p(1-\hat p))/(n) }=0.225\pm1.96* \sqrt{(0.225(1-0.225)/(120) }\\=0.225\pm 0.075\\=(0.15, 0.30)`

Thus, the 95% confidence interval for the proportion of children not overdue for vaccination is (0.15, 0.30).