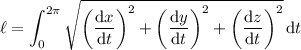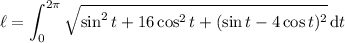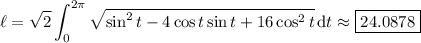Question

Find, correct to four decimal places, the length of the curve of intersection of the cylinder 16x2 + y2 = 16 and the plane x + y + z = 12.

Answer 1

First find a parameterization for the curve of intersection.

Given the equation of a cylinder, a natural choice for a parameterization would be one utilizing cylindrical coordinates. Here,

`16x^2+y^2=16\implies x^2+\left(\frac y4\right)^2=1`

which suggests we could use

`\begin{cases}x(t)=\cos t\\y(t)=4\sin t\\z(t)\end{cases}`

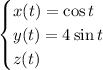
with
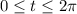`0\le t\le2\pi`, and we get
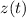`z(t)` from the equation of the plane,

`x+y+z=12\implies z(t)=12-x(t)-y(t)=12-\cos t-4\sin t`

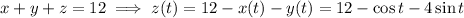
Now use the arc length formula:

`\displaystyle\ell=\int_0^(2\pi)\sqrt{\left((\mathrm dx)/(\mathrm dt)\right)^2+\left((\mathrm dy)/(\mathrm dt)\right)^2+\left((\mathrm dz)/(\mathrm dt)\right)^2}\,\mathrm dt`

`\displaystyle\ell=\int_0^(2\pi)√(\sin^2t+16\cos^2t+(\sin t-4\cos t)^2)\,\mathrm dt`

`\displaystyle\ell=\sqrt2\int_0^(2\pi)√(\sin^2t-4\cos t\sin t+16\cos^2t)\,\mathrm dt\approx\boxed{24.0878}`