Answer:
(a) The probability distribution is shown in the attachment.
(b) The value of E (Y) is 7.85.
(c) The value of E (X) and E (X²) are 1.45 and 3.25 respectively.
(d) The value of P (Y ≤ 2) is 0.60.
(e) Verified that the value of E (Y) is 7.85.
Explanation:
(a)
The random variable Y is defined as:
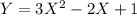
For X = {0, 1, 2, 3} the value of Y are:

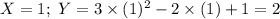
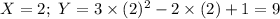
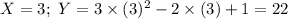
The probability of Y for different values are as follows:
P (Y = 1) = P (X = 0) = 0.20
P (Y = 2) = P (X = 1) = 0.40
P (Y = 9) = P (X = 2) = 0.15
P (Y = 22) = P (X = 3) = 0.25
The probability distribution of Y is shown below.
(b)
The expected value of a random variable using the probability distribution table is:
![E(U)=\sum[u* P(U=u)]](https://img.qammunity.org/2021/formulas/mathematics/college/gdwan0zlt32whskrs5f97h71ojcz87ptgx.png)
Compute the expected value of Y as follows:
![E(Y)=\sum [y* P(Y=y)]\\=(1*0.20)+(2*0.40)+(9*0.15)+(22*0.25)\\=7.85](https://img.qammunity.org/2021/formulas/mathematics/college/cewfccafvb2ezlj12nvhvrl194xvtoza15.png)
Thus, the value of E (Y) is 7.85.
(c)
Compute the expected value of X as follows:
![E(X)=\sum [x* P(X=x)]\\=(0*0.20)+(1*0.40)+(2*0.15)+(3*0.25)\\=1.45](https://img.qammunity.org/2021/formulas/mathematics/college/8w5193zi84ze8sptv8b3ytpk1ujrcojem8.png)
Compute the expected value of X² as follows:
![E(X^(2))=\sum [x^(2)* P(X=x)]\\=(0^(2)*0.20)+(1^(2)*0.40)+(2^(2)*0.15)+(3^(2)*0.25)\\=3.25](https://img.qammunity.org/2021/formulas/mathematics/college/ft1evrvbwxyhpsxa5qqupnyci48bay4lsj.png)
Thus, the value of E (X) and E (X²) are 1.45 and 3.25 respectively.
(d)
Compute the value of P (Y ≤ 2) as follows:
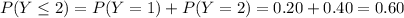
Thus, the value of P (Y ≤ 2) is 0.60.
(e)
The value of E (Y) is 7.85.
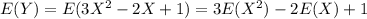
Use the values of E (X) and E (X²) computed in part (c) to compute the value of E (Y).

Hence verified.