Question

ANSWER CORRECTLY OR DONT ANSWER AT ALL

Answer 1

5) A

6) C

7) B

8) D

9) D

10) A

11) C

12) C

Explanation:

5) The graph of an exponential decay function approaches zero, as the values of x grows bigger and bigger.

From the graph, it is only the first graph the has the end behavior of an exponential decay function.

The correct answer is A) I only

6) The given function is
`y=2(3^x)`.

From x=1 to x=3, the grows by a factor of
`3^(3-1)=3^2=9`

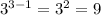
From x=5 to x=7, the exponential function grows by a factor of
`3^(7-5)=3^(2)=9`

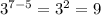
The correct answer is C.

7) The initial value of the car is $20,000.

Since the car loses 20% of its value every year, it has a multiplicative rate of change of
`r=(4)/(5)`

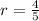
Hence the value will decay exponentially.

The correct answer is B.

8) Let the initial population be
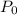`P_0`, then after 210 minutes,
`P=2P_0`

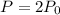
This implies that:
`2P_0=P_0e^(210k)`

`\implies k=(\ln(2))/(210)`

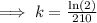
With initial population is
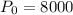`P_0=8000`, we want to find the population after 630 minutes.

`P=8000e^{(\ln(2))/(210)*630}=64000`

The correct answer is D

9)

Let the initial population be
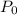`P_0`, then after 60 minutes,
`P=3P_0`

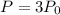
This implies that:
`3P_0=P_0e^(60k)`

`\implies k=(\ln(3))/(60)`

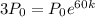
With initial population is
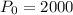`P_0=2000`, we want to find the population after 240 minutes.

`P=2000e^{(\ln(3))/(60)*240}=162000`

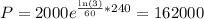
The correct answer is D

10) The initial cost is $40 the unit rate per visit to the Gym is

$2

The total cost y, is given by:
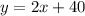`y=2x+40`, where x is the number of visit.

With $90, you substitute y=90 and solve for x.

`2x+40=90`

`2x=50\\x=25`

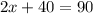
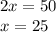
The correct answer is A

11) Let
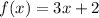`f(x)=3x+2`, then
`f(x+2)=3(x+2)+2=3x+6+2=3x+8`

`f(a+2)-f(a)=3a+8-(3a+2)=3a+8-3a-2=6`

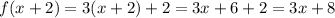
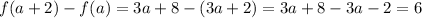
Therefore the correct answer is C.
`y=3x+2`

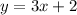
12) Let
`f(x)=7(0.5)^x`, then
`f(x+2)=7(0.5)^(x+2)`

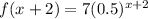
This implies that:

`(f(a+2))/(f(a))=(7(0.5)^(x+2))/(f(7(0.5)^(x))= (7(0.5)^(x)*0.5^2)/(f(7(0.5)^(x))=(0.5^2)/(1)=(1)/(4)`

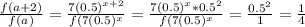
The correct answer is C