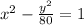Question

What is the equation of a hyperbola with a = 1 and c = 9? Assume that the transverse axis is horizontal.

Answer 1

Explanation:

The general formula for a horizontal hyperbola :

`(x^(2) )/(a^(2) ) -(y^(2) )/(b^(2) ) =1`

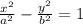
Given: a = 1 we know a² = 1 ,and that c = 9 so we know c² = 9² = 81

We also know that the relation between a, b, c for a hyperbola is c²= a²+b²

c²= a²+b², substitute what we know

81 = 1 +b², subtract 1 from both sides of the equation

80 = b²

The equation of our hyperbola is:

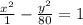`(x^(2) )/(1 ) -(y^(2) )/(80 ) =1` or
`x^(2) -(y^(2) )/(80) =1`