Question

A ball of mass m is thrown straight upward from ground level at speed v0. At the same instant, at a distance D above the ground, another ball of mass m is thrown straight downward toward the first ball, also at speed v0. Assume that gravity acts vertically downward on each mass m with a magnitude mg.

Answer 1

a.
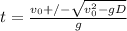`t = \frac{v_(0) +/- \sqrt{v_(0) ^(2) - gD} }{g}` b. D = v₀²/2g

Step-by-step explanation:

Here is the complete question

A ball is thrown straight up from the ground with speed v₀ . At the same instant, a second ball is dropped from rest from a height D , directly above the point where the first ball was thrown upward. There is no air resistance

Find the time at which the two balls collide.

Express your answer in terms of the variables D ,v₀ , and appropriate constants..

t = ?!

Part B

Find the value of D in terms of v₀ and g so that at the instant when the balls collide, the first ball is at the highest point of its motion.

Express your answer in terms of the variables v₀ and g .

D =?!

Solution

The distance moved by the ball dropped from distance,D with velocity v₀, H₁ = D - (v₀t - gt²/2) = D + v₀t + gt²/2.

The distance moved by the ball thrown straight upward with velocity v₀ is H₂ = v₀t - gt²/2.

The two balls collide when their vertical distances are equal. That is H₁ = H₂

So, D - v₀t + gt²/2 = v₀t - gt²/2

Collecting like terms

D + gt²/2 + gt²/2 = v₀t + v₀t

D +gt² = 2v₀t

gt² - 2v₀t + D = 0.

Using the quadratic formula,

`t = \frac{-(-2v_(0) ) +/- \sqrt{(-2v_(0) )^(2) - 4 X g XD} }{2g} = \frac{2v_(0) +/- \sqrt{4v_(0) ^(2) - 4gD} }{2g} = \frac{v_(0) +/- \sqrt{v_(0) ^(2) - gD} }{g}`

B. At its highest point, the velocity of the first ball, v = 0. Using v² = u² - 2gs where s = highest point of first ball when they collide and u = v₀.

0 = v₀² - 2gs

s = v₀²/2g.

Also, the time it takes the first ball to reach its highest point is gotten from v = u - gt. At highest point, v = 0 and u = v₀. So,

0 = v₀ - gt₀

t₀ = v₀/g

Also H = s₁ + s where s₁ = distance moved by second ball in time t₀ for collision = v₀t₀ - gt₀²/2.

So, H = v₀t₀ - gt₀²/2 + v₀²/2g = v₀(v₀/g) - g(v₀/g)²/2 + v₀²/2g = v₀²/2g - v₀²/2g + v₀²/2g = v₀²/2g