Answer:
1) +3.30 μC 2) -8.60 μC 3) 6.31*10⁷ N/C
Step-by-step explanation:
1) Applying Gauss´Law to a gaussian spherical surface with a radius between the inner radius of the shell, and the outer radius, we find that the net flux through this surface is just zero:
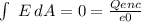
This is due to no electric field can exist inside a conductor in electrostatic condition.
So, if the left side of the equation is 0, the right side must be zero too:
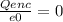
If the total charge enclosed by the gaussian surface is 0, and we have a charge of -3.30 μC in the center, there must exist a +3.30 μC, on the inner surface of the shell, so the total charge be 0.
⇒ Qin = +3.30 μC
2) As the charge must be conserved, if the net charge of the shell is -5.30 μC, if we have +3.30 μC on the inner surface, we will have a charge on the outer surface, that keep the total charge of the shell constant, as follows:
Qou = Qsh - Qin = -5.30 μC -(+3.30 μC) = -8.60 μC
3) In order to find the electric field just outside the shell, we can apply Gauss' Law to a gaussian spherical surface of radius equal to the outer shell radius.
By symmetry, as the electric field must be radial, at a same radius, the magnitude of the electric field must be the same. As the dA vector is normal to the surface, is also radial, so we can write Gauss´ Law as follows:
E* 4*π*r² = Qenc / ε₀
where Qenc = Qc + Qin + Qou
As Qc+ Qin = 0, ⇒ Qenc =Qou = -8.60 μC
r = distance to the center of the sphere = 3.5 cm = 0.035 m
ε₀ = 8.85*10⁻¹² C²/N*m²
Replacing by the values, we can solve for E, as follows:
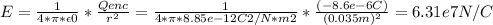
⇒ E = 6.31*10⁷ N/C