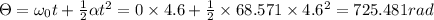Question

A uniform disk of mass M = 4.9 kg has a radius of 0.12 m and is pivoted so that it rotates freely about its axis. A string wrapped around the disk is pulled with a force F equal to 20 N.

(a) What is the torque being exerted by this force about the rotation axis?

(b) What is the angular acceleration of the disk?

(c) If the disk starts from rest, what is its angular speed after 4.6 s?

(d) What is its kinetic energy after the 4.6 s?

(e) What is the angular displacement of the disk during the 4.6 s?

Answer 1

(A) 2.4 N-m

(B)
`0.035kgm^2`

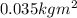
(C) 315.426 rad/sec

(D) 1741.13 J

(E) 725.481 rad

Step-by-step explanation:

We have given mass of the disk m = 4.9 kg

Radius r = 0.12 m, that is distance = 0.12 m

Force F = 20 N

(a) Torque is equal to product of force and distance

So torque
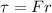`\tau =Fr`, here F is force and r is distance

So
`\tau =20* 0.12=2.4Nm`

(B) Moment of inertia is equal to
`I=(1)/(2)mr^2`

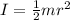
So
`I=(1)/(2)* 4.9* 0.12^2=0.035kgm^2`

Torque is equal to
`\tau =I\alpha`

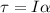
So angular acceleration
`\alpha =(\tau )/(I)=(2.4)/(0.035)=68.571rad/sec^2`

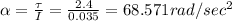
(C) As the disk starts from rest

So initial angular speed
`\omega _(0)=0rad/sec`

Time t = 4.6 sec

From first equation of motion we know that
`\omega =\omega _0+\alpha t`

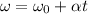
So
`\omega =0+68.571* 4.6=315.426rad/sec`

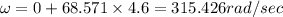
(D) Kinetic energy is equal to
`KE=(1)/(2)I\omega ^2=(1)/(2)* 0.035* 315.426^2=1741.13J`

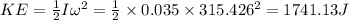
(E) From second equation of motion

`\Theta =\omega _0t+(1)/(2)\alpha t^2=0* 4.6+(1)/(2)* 68.571* 4.6^2=725.481rad`