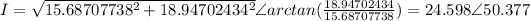Answer:
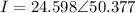
Step-by-step explanation:
A tension or current expressed in cosine form and with a positive sign can be converted directly into a phasor. This is done by indicating the tension and the offset angle:
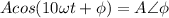
So:
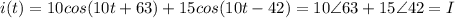
You can sum the phasors simply using a calculator, however, let's do it manually:
Let's find the rectangular form of each phasor using the next formulas:
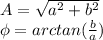
For
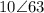
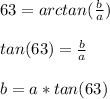
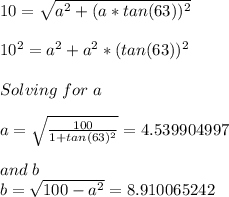
So:
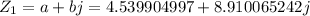
For
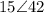
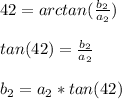
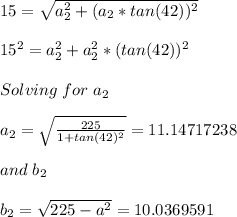
So:
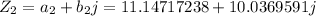
Hence:
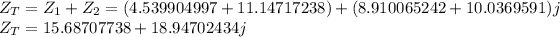
Finally: