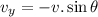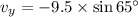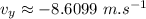Answer:
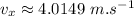
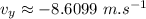
Step-by-step explanation:
Given:
initial speed of the hammer when leaving the edge of the roof along the inclination of the roof,
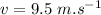
inclination of the roof form horizontal,
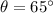
- Since the hammer is moving from the top of the roof to the right edge, its horizontal component will be towards right and vertical component will be towards downward direction.
Now the horizontal velocity:
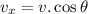
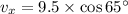
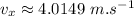
The vertical velocity: