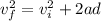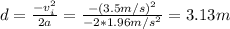Question

A stockroom worker pushes a box with mass 16.8 kg on a horizontal surface with a constant speed of 3.50 m/s. The coefficient of kinetic friction between the box and the surface is 0.20. (a) What horizontal force must the worker apply to maintain the motion? (b) If the force calculated in part (a) is removed, how far does the box slide before coming to rest?

Answer 1

a)
`fr =\mu N= 0.2*164.64 N= 32.928 N`

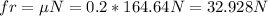
And we need a force
`F> 32.928 N[tex]</p><p>b) [tex] d = (-v^2_i)/(2a)= (-(3.5m/s)^2)/(-2*1.96 m/s^2)= 3.13m`

Step-by-step explanation:

Part a

For this case we have the following forces illustrated on the figure attached.

If we analyze on the x axis we just have two forces, fr the friction force and F the force to mantain the movement.

So we need this condition to satisfy the movement:

`F > fr`

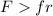
If we analyze the forces on the y axis we have this:

`\sum Fy= ma_y = 0`

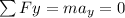
Because we have constant speed for this reason the acceleration is 0

`N -W = 0`

`N = mg = 16.8Kg * 9.8 (m)/(s^2)= 164.64 N`

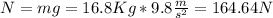
And by definition the friction force is defined as:
`fr = \mu N`

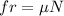
So then the friction force would be:

`fr =\mu N= 0.2*164.64 N= 32.928 N`

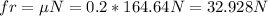
And we need a force
`F> 32.928 N`

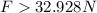
Part b

For this case we assume that F =0 and we have a friction force of 32.928 N.

From the second law of Newton we have:

`F = ma`

`a = (F)/(m)= -(fr)/(m)= -(32.928 N)/(16.8 Kg)= -1.96m/s^2`

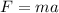
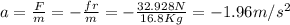
vf =0 (final velocity, rest at the end) and vi = 3.5 m/s.

And we can find the time for the motion like this:

`vf = v_i + at`

`t = (-v_i)/(a)= (-3.5 m/s)/(-1.96 m/s^2)= 1.78 s`

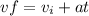
And then we can find the distance from the following formula:

`v^2_f= v^2_i + 2a d`

`d = (-v^2_i)/(2a)= (-(3.5m/s)^2)/(-2*1.96 m/s^2)= 3.13m`