Question

Determine the speed of sound in air at 400 K. Also determine the Mach number of an aircraft moving in the air at a velocity of 310 m/s.

The gas constant of air is R = 0.287 kJ/kg*K. Its specific heat ratio at room temperature is k = 1.4.

Answer 1

`\alpha = \sqrt{1.4 *0.287 (KJ)/(Kg K)*(1000J)/(1KJ) *400 K}= 400.899 m/s`

`Ma= (310 m/s)/(400.899 m/s)= 0.773`

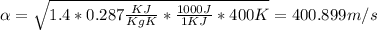
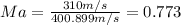
Step-by-step explanation:

For this case we have given the following data:

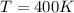`T= 400 K` represent the temperature for the air

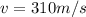`v = 310 m/s` represent the velocity of the air

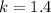`k = 1.4` represent the specific heat ratio at the room

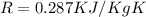`R = 0.287 KJ/ Kg K` represent the gas constant for the air

And we want to find the velocity of the air under these conditions.

We can calculate the spped of the sound with the Newton-Laplace Equation given by this equation:

`\alpha = \sqrt{(K)/(\rho)}=√(k RT)`

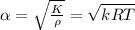
Where K = is the Bulk Modulus of air, k is the adiabatic index of air= 1.4, R = the gas constant for the air,
`\rho` the density of the air and T the temperature in K

So on this case we can replace and we got:

`\alpha = \sqrt{1.4 *0.287 (KJ)/(Kg K)*(1000J)/(1KJ) *400 K}= 400.899 m/s`

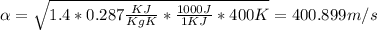
The Mach number by definition is "a dimensionless quantity representing the ratio of flow velocity past a boundary to the local speed of sound" and is defined as:

`Ma=(v)/(\alpha)`

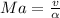
Where v is the flow velocity and
`\alpha` the volocity of the sound in the medium and if we replace we got:

`Ma= (310 m/s)/(400.899 m/s)= 0.773`

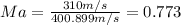
And since the Ma<0.8 we can classify the regime as subsonic.