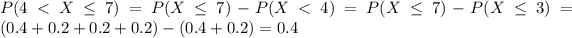Question

(1 point) An insurance company offers its policyholders a number of different premium payment options. For a randomly selected policyholder, let X be the number of months between successive payments. The CDF(cumulative distribution function) of X: F(x)=0, if x < 1,

F(x)=0.4, if 1 <_ x < 3,
F(x)=0.6, if 3 <_ x < 5,
F(x)=0.8, if 5 <_ x < 7,
F(x)=1.0, if x >_ 7.
(a) What is the probability mass function of X?
(b) Compute P(4 < X <_ 7) of X is __________.

Answer 1

a)

X | 1 3 5 7

f(X) | 0.4 0.2 0.2 0.2

b)
`P(4 <X \leq 7)= P(X\leq 7) -P(X<4) = P(X\leq 7) -P(X \leq 3) = (0.4+0.2+0.2+0.2) -(0.4+0.2)= 0.4`

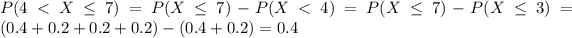
Explanation:

For this case we have defined the cumulative distribution function like this:

`F(X) = 0, x<1`

`F(X) = 0.4, 1 \leq x <3`

`F(X) = 0.6, 3 \leq x <5`

`F(X) = 0.8, 5 \leq x <7`

`F(X) = 1, x \geq 7`

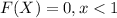
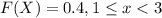
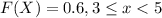
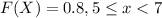
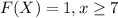
And we know that the general definition for the distribution function is given by:

`F(x) = P(X \leq x) = \sum_(i\leq k) f(i)`

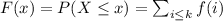
Where f represent the density function.

Part a

For this case we need to find the density function, so we can find the values for the density for each value of X = 1,2,3,4,5,6,7,... since X is a discrete random variable.

`f(1) = P(X=1) = P(X \leq 1) - P(X=0) = F(1) -F(0) = 0.4-0=0.4`

`f(2) = P(X=2) = P(X \leq 2) - P(X=0)- P(X=1) = F(2) -F(1) = 0.4-0.4=0`

`f(3) = P(X=3) = P(X \leq 3) - P(X=0)- P(X=1) -P(X=2) = F(3) -F(2) = 0.6-0.4=0.2`

`f(4) = P(X=4) = P(X \leq 4) - P(X=0)- P(X=1) -P(X=2)-P(X=3) = F(4) -F(3) = 0.6-0.6=0`

`f(5) = P(X=5) = P(X \leq 5) - P(X=0)- P(X=1) -P(X=2)-P(X=3)-P(X=4) = F(5) -F(4) = 0.8-0.6=0.2`

`f(6) = P(X=6) = P(X \leq 6) - P(X=0)- P(X=1) -P(X=2)-P(X=3)-P(X=4)-P(X=5) = F(6) -F(5) = 0.8-0.8=0`

`f(7) = P(X=7) = P(X \leq 7) - P(X=0)- P(X=1) -P(X=2)-P(X=3)-P(X=4)-P(X=5)-P(X=6) = F(7) -F(6) = 1-0.8=0.2`

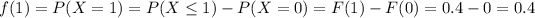
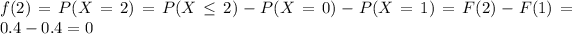
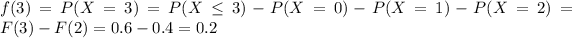
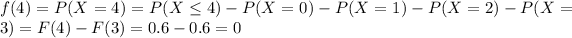
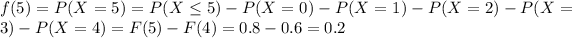
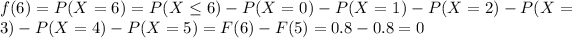
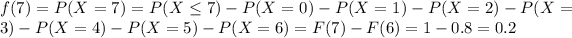
And for any value higher than 7 we have that:

`x_i \in [8,9,10,...]`

`f(x_i) = F(X_i) -F(X_i -1) = 1-1=0`

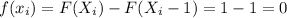
So then we have our density function defined like this:

X | 1 3 5 7

f(X) | 0.4 0.2 0.2 0.2

Part b

For this case we want to find this probability
`P(4 <X \leq 7)`

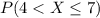
And since the random variable is discrete we can write this like that:

`P(4 <X \leq 7)= P(X\leq 7) -P(X<4) = P(X\leq 7) -P(X \leq 3) = (0.4+0.2+0.2+0.2) -(0.4+0.2)= 0.4`