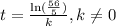Question

Biologists stocked a lake with 500 fish and estimated the environmental carrying capacity to be 6100. The number of fish doubled in the first year. Assume that the size of the fish population satisfies the logistic equation dPdt=kP(1−PK), where t is measured in years. Find an expression for the size of the population. Hint: Use partial fraction decomposition to solve for P. k= P= $$ How long will it take for the population to increase to 3050 (half of the carrying capacity)? It will take $$ years.

Answer 1

`P(t)=(38125e^(kt))/(7(1+(5)/(56) e^(kt)))`

Explanation:

The size of fish population satisfies the logistic equation:

`(dP)/(dt) =kP(1-(P)/(K))`

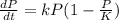
K=6100 is the carry capacity. Substitute to get:

`(dP)/(dt) =kP(1-(P)/(6100))`

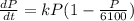
We separate variables to obtain:

`(6100dP)/(P(6100-P)) =k\cdot dt`

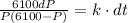
Use partial fraction decomposition to get:

`(dP)/(P)+(dP)/(6100-P) =k\cdot dt`

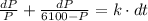
Integrate to obtain:

`\ln (|P|)/(|6100-P)=kt+C_1`

`\implies (P)/(6100-P) =Ce^(kt)------(1)`

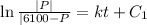
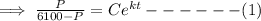
We apply the ICs to get,
`C=(5)/(56)`

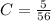
The expression for population size is

`P(t)=(6100*(5)/(6) e^(kt))/(1+(5)/(6) e^(kt))`

`P(t)=(38125e^(kt))/(7(1+(5)/(56) e^(kt)))`

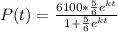
b)

Substitute P=3050 into
`(P)/(6100-P) =Ce^(kt)`

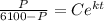
This implies that:

`\implies (3050)/(6100-3050) =(5)/(56) e^(kt)`

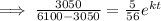
Solve for t to get:

`t=(\ln((56)/(5) ))/(k) ,k\\e 0`