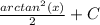Answer:
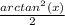
Explanation:
For this question, set u = arctan(x). This would be the easiest way because the derivative of arctan(x) is
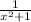 which is what we have. Before setting u, always look at the question and think about possible derivatives.
which is what we have. Before setting u, always look at the question and think about possible derivatives.
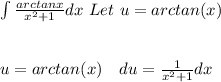
Next, plug in u and du.
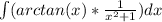 (rearranging)
(rearranging)
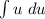
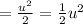
Substitute arctan(x) back in for u and add +C.