Question

A galvanic cell at a temperature of 42 degrees Celcius is powered by the following redox reaction:

3CU2+(aq)+2Al(s)-->3Cu(s)+2Al3+(aq)

Suppose the cell is prepared with 3.43 M Cu2+n one half-cell and 1.63 M Al3+in the other.

Calculate the cell voltage under these conditions. Round your answer to 3 significant digits.

Answer 1

Answer: The cell voltage of the given cell is 2.01

Step-by-step explanation:

The given chemical cell equation follows:

`3Cu^(2+)(aq.)+2Al(s)\rightarrow 3Cu(s)+2Al^(3+)(aq.)`

Oxidation half reaction:
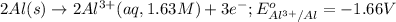`2Al(s)\rightarrow 2Al^(3+)(aq,1.63M)+3e^-;E^o_(Al^(3+)/Al)=-1.66V` ( × 2)

Reduction half reaction:
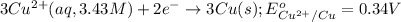`3Cu^(2+)(aq,3.43M)+2e^-\rightarrow 3Cu(s);E^o_(Cu^(2+)/Cu)=0.34V` ( × 3)

Oxidation reaction occurs at anode and reduction reaction occurs at cathode.

To calculate the
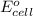`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

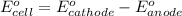
Putting values in above equation, we get:

`E^o_(cell)=0.34-(-1.66)=2.00V`

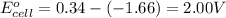
To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(2.303RT)/(nF)\log ([Al^(3+)]^2)/([Cu^(2+)]^3)`

where,

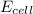`E_(cell)` = electrode potential of the cell = ? V

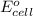`E^o_(cell)` = standard electrode potential of the cell = +2.00 V

R = Gas constant = 8.314 J/mol.K

T = temperature =
`42^oC=[42+273]K=315K`

F = Faraday's constant = 96500

n = number of electrons exchanged = 6

`[Cu^(2+)]=3.43M`

`[Al^(3+)]=1.63M`

Putting values in above equation, we get:

`E_(cell)=2.00-(2.303* 8.314* 315)/(6* 96500)* \log(((1.63)^2)/((3.43)^3))`

`E_(cell)=2.01`

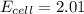
Hence, the cell voltage of the given cell is 2.01