Question

Working alone, Jess can rake leaves off a lawn in 50 minutes. Working alone, cousin Tate can do the same job in 30 minutes. Today they are going to work together, Jess starting t one end of the lawn and Tate starting simultaneously at the other end. In how many minutes will they meet and thus have the lawn completely raked?

Answer 1

18.75 minutes.

Explanation:

Let t represent minutes taken to complete the job by Jess and Tate working together.

We have been given that working alone, Jess can rake leaves off a lawn in 50 minutes, so part of work done by Jess in 1 minute would be
`(1)/(50)`.

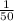We are also told that working alone, cousin Tate can do the same job in 30 minutes, so part of work done by Tate in 1 minute would be
`(1)/(30)`.

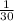Part of work done by both in one minute would be
`(1)/(t)`.

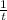We can represent our given information in an equation as:

`(1)/(50)+(1)/(30)=(1)/(t)`

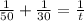
Let us solve for t.

`(1)/(50)*150t+(1)/(30)*150t=(1)/(t)*150t`

`3t+5t=150\\\\8t=150`

`(8t)/(8)=(150)/(8)\\\\t=18.75`

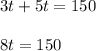
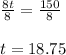
Therefore, the lawn will be completely raked in 18.75 minutes and they will meet after 18.75 minutes.