Answer:
a)
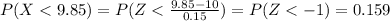
And for the other case:
tex] P(X>10.15)[/tex]
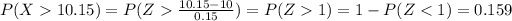
So then the probability of being defective P(D) is given by:
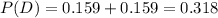
And the expected number of defective in a sample of 1000 units are:
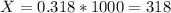
b)
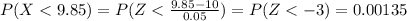
And for the other case:
tex] P(X>10.15)[/tex]
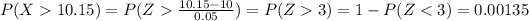
So then the probability of being defective P(D) is given by:
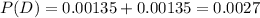
And the expected number of defective in a sample of 1000 units are:
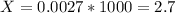
c) For this case the advantage is that we have less items that will be classified as defective
Explanation:
Assuming this complete question: "Motorola used the normal distribution to determine the probability of defects and the number of defects expected in a production process. Assume a production process produces items with a mean weight of 10 ounces. Calculate the probability of a defect and the expected number of defects for a 1000-unit production run in the following situation.
Part a
The process standard deviation is .15, and the process control is set at plus or minus one standard deviation. Units with weights less than 9.85 or greater than 10.15 ounces will be classified as defects."
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Solution to the problem
Let X the random variable that represent the weights of a population, and for this case we know the distribution for X is given by:
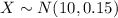
Where
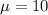 and
and
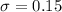
We can calculate the probability of being defective like this:
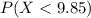
And we can use the z score formula given by:
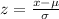
And if we replace we got:
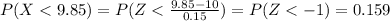
And for the other case:
tex] P(X>10.15)[/tex]
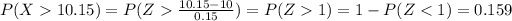
So then the probability of being defective P(D) is given by:
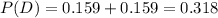
And the expected number of defective in a sample of 1000 units are:
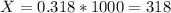
Part b
Through process design improvements, the process standard deviation can be reduced to .05. Assume the process control remains the same, with weights less than 9.85 or greater than 10.15 ounces being classified as defects.
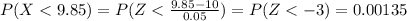
And for the other case:
tex] P(X>10.15)[/tex]
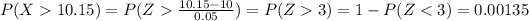
So then the probability of being defective P(D) is given by:
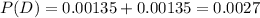
And the expected number of defective in a sample of 1000 units are:
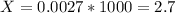
Part c What is the advantage of reducing process variation, thereby causing process control limits to be at a greater number of standard deviations from the mean?
For this case the advantage is that we have less items that will be classified as defective