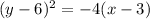Answer:
1.

2.
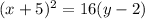
3.
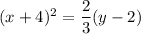
4. See explanation
5.
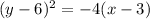
Explanation:
1. The equation of given parabola is
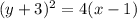
The vertex of this parabola is at point (1,-3), this parabola goes in positive x-direction and has the parameter
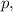 such that
such that

The directrix is the vertical line. The equation of the directrix is
![x-x_0=-(p)/(2)\ [x_0\text{ is the x-coordinate of the vertex}]\\ \\x-1=-(2)/(2)\\ \\x-1=-1\\ \\x=0](https://img.qammunity.org/2021/formulas/mathematics/middle-school/c757tkq77axsdvdq6bj9jm0tl9299mrdq9.png)
2. The vertex of the parabola is at point (-5,2), the focus is at point (-5,6), this means that the vertex and the focus both lie on the vertical line x = -5. This line is the line of symmetry of the parabola. Thus, parabola goes in positive y-direction and has the equation
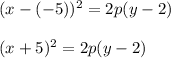
To find the parameter
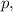 note that the distance between vertex and focus is equal to
note that the distance between vertex and focus is equal to
 hence,
hence,
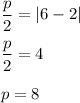
and the equation of the parabola is
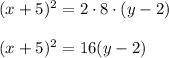
3. Given the equation
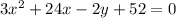
Rewrite this equation as follows
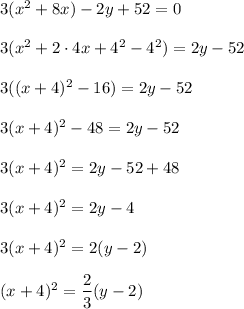
4. Given the equation of the parabola
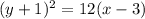
The vertex of the parabola is at point (3,-1).
The parabola opens to the right.
Parabola's parameter is
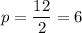 , so the focus is
, so the focus is
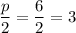 units away from the vertex.
units away from the vertex.
The directrix is
 units away from the focus.
units away from the focus.
The focus is at the point
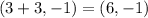 and the directrix has the equation
and the directrix has the equation
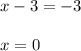
5. The distance between the directrix and the focus is
 units.
units.
The directrix is to the right from the focus, so parabola opens to the left and has the equation

where
 is the vertex.
is the vertex.
The vertex is the point that is half way from the focus to the directrix, hence

So, the equation is