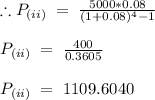Question

You want to take a dream vacation in 3.5 years. You plan to save up $5,000 in your vacation sinking fund. Assume an interest rate of 8% compounded annually. How much will you have to save if you make a lump sum deposit to the sinking fund (i) during the year or (ii) at the beginning of the year?

Answer 1

Step-by-step explanation:

The formula for calculating the Monthly payments P for the sinking fund is as follows:

`P\;=\;(A*i)/((1+i)^n-1)`

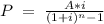
where,

P = Monthly payments to be made

A = Total amount to be accumulated

i = Interest rate for given time period

n = Number of time period

Assuming interest is applied at the beginning of each period.

We are given two scenarios.

Scenario (i) - Deposit is made during the year:

In this scenario, as some of the year is already passed (assume 6 months), to complete the time period of 3.5 years the interest will compound 3 times (as the 0.5 year payments can be adjusted in the remaining part of the first year and no interest is applied on it). Hence, the interest will be applied 3 times.

`\therefore P_((i))\;=\;(5000*0.08)/((1+0.08)^3-1)\\\\P_((i))\;=\;(400)/(0.2597)\\\\P_((i))\;=\;1540.1676`

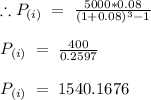
Scenario (ii) - Deposit is made at the beginning of the year:

For this case, the interest will be applied 4 times to complete the time period of 3.5 years for payment.

`\therefore P_((ii))\;=\;(5000*0.08)/((1+0.08)^4-1)\\\\P_((ii))\;=\;(400)/(0.3605)\\\\P_((ii))\;=\;1109.6040`