Question

A reaction A ( aq ) + B ( aq ) − ⇀ ↽ − C ( aq ) has a standard free‑energy change of − 5.43 kJ / mol at 25 °C. What are the concentrations of A , B , and C at equilibrium if, at the beginning of the reaction, their concentrations are 0.30 M, 0.40 M, and 0 M, respectively?

Answer 1

To find the equilibrium concentrations of A, B, and C, one must calculate the equilibrium constant from the given standard free-energy change, and then apply the ICE table methodology, considering stoichiometry and initial concentrations.

Step-by-step explanation:

The student has asked about determining the concentrations of reactants and products at equilibrium for a given chemical reaction with a known standard free-energy change. To solve this, we use the fact that the equilibrium constant (Kc) can be calculated from the standard free-energy change (ΔG°) using the formula Kc = e(-ΔG°/RT), where R is the ideal gas constant and T is the temperature in Kelvin.

Using the initial concentrations given and the calculated Kc, we can apply the ICE (Initial, Change, Equilibrium) table approach to determine the changes in concentrations as the reaction moves towards equilibrium. With the stoichiometry of the reaction A (aq) + B (aq) ⇌ C (aq) and the provided starting concentrations, changes in concentration (±x) due to the shift in equilibrium are reflected in the ICE table, allowing us to solve for the equilibrium concentrations of A, B, and C.

Answer 2

Answer : The concentrations of A, B, and C at equilibrium is, 0.11 M, 0.21 M and 0.19 M respectively.

Explanation :

The relation between the equilibrium constant and standard Gibbs, free energy is:

`\Delta G^o=-RT* \ln K`

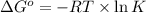
where,

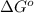`\Delta G^o` = standard Gibbs, free energy = -5.43 kJ/mol = -5430 J/mol

R = gas constant = 8.314 J/mol.K

T = temperature =
`25^oC=273+25=298K`

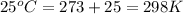
K = equilibrium constant = ?

Now put all the given values in the above relation, we get:

`-5430J/mol=-(8.314J/mol.K)* (298K)* \ln K`

`K=8.95`

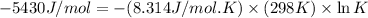
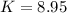
Now we have to calculate the concentrations of A, B, and C at equilibrium.

The balanced equilibrium chemical reaction is:

`A(aq)+B(aq)\rightleftharpoons C(aq)`

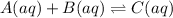
Initial conc. 0.30 0.40 0

At eqm. (0.30-x) (0.40-x) x

The expression for equilibrium constant for this reaction is,

`K=([C])/([A][B])`

Now put all the given values in this expression, we get:

`8.95=(x)/((0.30-x)* (0.40-x))`

`x=0.19\text{ and }0.62M`

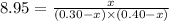
As we know that the concentration at equilibrium can not be more than initial concentration. So, neglecting the value of x = 0.62 M

The value of 'x' will be, 0.19 M

Thus, the concentrations of A at equilibrium = (0.30-x) = (0.30-0.19) = 0.11 M

The concentrations of B at equilibrium = (0.40-x) = (0.40-0.19) = 0.21 M

The concentrations of C at equilibrium = x = 0.19 M