The coordinates of the point that partitions PT is (5, 11).
Solution:
Given P(2, 2) and T(7, 17).
Line segment PT is divided the coordinates of the point in the ratio 3 : 2.
Let R be the divided point the line segment PT.
Section Formula:
The point (x, y) which divides the line segment of the points
 and
and
 in the ratio m : n is
in the ratio m : n is
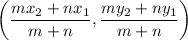
Here
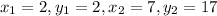 and m = 3, n = 2
and m = 3, n = 2
Substitute these in the given formula.
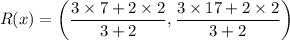
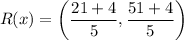

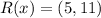
Hence the coordinates of the point that partitions PT is (5, 11).