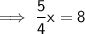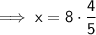Answer:
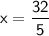
(or x = 6.4 if you want it in decimal form)
Explanation:
If y and x have a proportional relationship, then:
- y = kx (for some constant k)
Given:
Substitute the given values into the equation to find k:
⇒ 5 = k(4)
⇒ k = 5/4
Therefore,
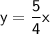
When y = 8, substitute y = 8 into the equation and solve for x: