Question

The arrival of the city busses that trundle down my street is Poisson distributed. According to the published schedule, they arrive every 10 minutes. What is the probability that exactly two such busses arrive within 3 minutes of each other

Answer 1

There is a 3.33% probability that exactly two such busses arrive within 3 minutes of each other.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

What is the probability that exactly two such busses arrive within 3 minutes of each other

The mean is one bus each 10 minutes. So for 3 minutes, the mean is 3/10 = 0.3 buses. So we use
`\mu = 0.3`

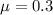
This probability is P(X = 2).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 2) = (e^(-0.3)*(0.3)^(2))/((2)!) = 0.0333`

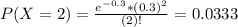
There is a 3.33% probability that exactly two such busses arrive within 3 minutes of each other.