Answer:
Radius of orbit = 3.992 ×
 m
m
Altitude of Satellite =33541.9× m
Step-by-step explanation:
Formula for gravitational force for a satellite of mass m moving in an orbit of radius r around a planet of mass M is given by;
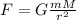
Where G = Gravitational constant = 6.67408 × 10-11
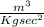
We are given
F= 800 N
m = 320 Kg
M = 5.972 ×
 Kg
Kg
G = 6.67408 × 10-11
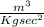
We have to find radius r =?
putting values in formula;
==> 800 =6.67408 ×
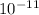 × 320 × 5.972 ×
× 320 × 5.972 ×
 /
/

==> 800= 39.8576 ×
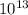 × 320 /
× 320 /

==> 800 = 12754.43 ×
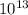 /
/

==>
 = 12754.43 ×
= 12754.43 ×
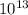 /800
/800
==>
 =15.94 ×
=15.94 ×
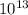
==> r = 3.992 ×
 m
m
==> r = 39920×
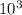 m
m
This is the distance of satellite from center of earth. To find altitude we need distance from surface of earth. So we will subtract radius of earth from this number to find altitude.
Radius of earth =6378.1 km = 6378.1 ×
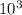 m
m
Altitude = 39920×
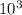 - 6378.1 ×
- 6378.1 ×