Question

Camila designed two different dog pens. The smaller dog pen is a scale drawing of the larger one. If the

perimeter of the larger dog pen is 150 feet, then the perimeter of the smaller dog pen is
—————feet

Answer 1

Answer:
`56.25\ ft`

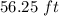
Explanation:

The first step to solve this exercise is to find the the ratio of the figure's corresponding sides, which is called the "Scale factor".

You can observe in the picture that the dog pens have the shape of trapezoids.

Assuming that the squares of the grid have side lengths of 1 feet, you can identify that the large base of the larger trapezoid has the following length:

`B_l=8\ ft`

And the large base of the of the smaller trapezoid is:

`B_s=3\ ft`

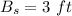
Then, the scale factor used to get the smaller trapezoid is:

`scale\ factor=(3)/(8)`

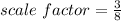
Knowing that the perimeter of the larger dog pen is 150 feet, you can set up the following proportion, where "p" is the perimeter of the smaller one:

`(3)/(8)=(p)/(150)`

Solving for "p", you get:

`(150)((3)/(8))=p\\\\p=56.25\ ft`