Question

The vapor pressure of ethanol is 1.00 × 102 mmHg at 34.90°C. What is its vapor pressure at 60.61°C? (ΔHvap for ethanol is 39.3 kJ/mol.) mmHg

Answer 1

The vapor pressure of ethanol at 60.61 °C is 327.56 mmHg

Step-by-step explanation:

using Clausius-Clapeyron equation

`ln((P_2)/(P_1)) = (\delta H)/(R)((1)/(T_1) -(1)/(T_2))`

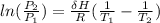
where;

ΔH is the enthalpy of vaporization of ethanol = 39.3 kJ/mol

R is ideal gas constant = 8.314 J/mol.K

P₁ is the initial pressure of ethanol at T₁ = 1.00 × 10² mmHg

P₂ is the final pressure of ethanol at T₂ = ?

T₁ is the initial temperature = 34.9°C = 307.9 K

T₂ is the final temperature = 60.61°C = 333.61 K

`ln((P_2)/(P_1)) = (\delta H)/(R)((1)/(T_1) -(1)/(T_2)) \\\\ln((P_2)/(100)) = (39300)/(8.314)((1)/(307.9) -(1)/(333.61))\\\\ln((P_2)/(100)) = 4726.9666 (0.003248 -0.002997)\\\\ln((P_2)/(100)) = 4726.9666 (0.000251) = 1.1865\\\\((P_2)/(100)) = e^((1.1865)) \\\\((P_2)/(100)) = 3.2756\\\\P_2 = (100*3.2756)mmHg\\\\P_2 = 327.56 mmHg`

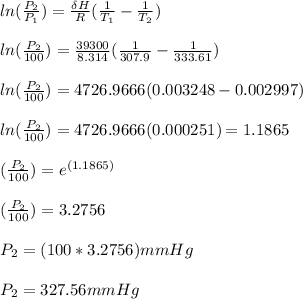
Therefore, the vapor pressure of ethanol at 60.61 °C is 327.56 mmHg