Question

Problem PageQuestion An analytical chemist is titrating of a solution of nitrous acid with a solution of . The of nitrous acid is . Calculate the pH of the acid solution after the chemist has added of the solution to it. Note for advanced students: you may assume the final volume equals the initial volume of the solution plus the volume of solution added. Round your answer to decimal places.

Answer 1

The question is incomplete, here is the complete question:

An analytical chemist is titrating 182.2 mL of a 1.200 M solution of nitrous acid with a solution of 0.8400 M KOH. The
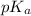`pK_a` of nitrous acid is 3.35. Calculate the pH of the acid solution after the chemist has added 46.44 mL of the KOH solution to it. Note for advanced students: you may assume the final volume equals the initial volume of the solution plus the volume of solution added. Round your answer to 2 decimal places.

Answer: The pH of the solution is 2.69

Step-by-step explanation:

To calculate the number of moles for given molarity, we use the equation:

`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in mL)}}`

• For nitrous acid:

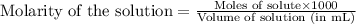
Molarity of nitrous acid = 1.200 M

Volume of solution = 182.2 mL

Putting values in above equation, we get:

`1.200M=\frac{\text{Moles of nitrous acid}* 1000}{182.2mL}\\\\\text{Moles of nitrous acid}=(1.200* 182.2)/(1000)=0.219mol`

• For KOH:

Molarity of KOH = 0.8400 M

Volume of solution = 46.44 mL

Putting values in above equation, we get:

`0.8400M=\frac{\text{Moles of KOH}* 1000}{46.44mL}\\\\\text{Moles of KOH}=(0.8400* 46.44)/(1000)=0.039mol`

The chemical reaction for KOH and nitrous acid follows the equation:

`HNO_2+KOH\rightarrow KNO_2+H_2O`

Initial: 0.219 0.039

Final: 0.18 - 0.039

Volume of solution = 182.2 + 46.44 = 228.64 mL = 0.22864 L (Conversion factor: 1 L = 1000 mL)

To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:

`pH=pK_a+\log(([salt])/([acid]))`

`pH=pK_a+\log(([KNO_2])/([HNO_2]))`

We are given:

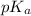`pK_a` = negative logarithm of acid dissociation constant of nitrous acid = 3.35

`[KNO_2]=(0.039)/(0.22864)`

`[HNO_2]=(0.18)/(0.22864)`

pH = ?

Putting values in above equation, we get:

`pH=3.35+\log((0.039/0.22864)/(0.18/0.22864))\\\\pH=2.69`

Hence, the pH of the solution is 2.69