Question

Two points in a plane have polar coordinates (3.00 m, 20.0°) and (3.50 m, 140.0°). (a) Determine the Cartesian coordinates of these points. (3.00 m, 20.0°) x = m y = m (3.50 m, 140.0°) x = m y = m (b) Determine the distance between them.

Answer 1

(a) Cartesian coordinate (2.8191m, 1.0260m) and (-2.6810m, 2.2498m)

(b) distance = 5.6346m

Step-by-step explanation:

Given a polar coordinate (r, θ);

Its Cartesian coordinate is (x, y) where;

x = r cos θ

y = r sin θ

Now, given the polar coordinate (3.00, 20.0⁰)

Its Cartesian coordinate is (x, y) where

x = 3.00 cos 20.0° = 3.00 x 0.9397 = 2.8191m

y = 3.00 sin 20.0° = 3.00 x 0.3420 = 1.0260m

Therefore,

Polar coordinate (3.00m, 20.0°) = Cartesian coordinate (2.8191m, 1.0260m)

Also,

Now, given the polar coordinate (3.50, 140.0⁰)

Its Cartesian coordinate is (x, y) where

x = 3.50 cos 140.0° = 3.50 x -0.7660 = -2.6810m

y = 3.40 sin 140.0° = 3.50 x 0.6428 = 2.2498m

Therefore,

Polar coordinate (3.50m, 140.0°) = Cartesian coordinate (-2.6810m, 2.2498m)

(a) Polar coordinates (3.00m, 20.0°) and (3.50m, 140.0°) = Cartesian coordinate (2.8191m, 1.0260m) and (-2.6810m, 2.2498m)

(b) To calculate the distance between them, it is easier to use the values from the Cartesian representation as follows;

distance =
`\sqrt{(x_(2) - x_(1))^(2) + (y_(2) - y_(1))^(2) }`

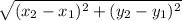
where;

(
`x_(1)`,
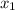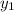`y_(1)`) = (2.8191m, 1.0260m) and

(
`x_(2)`,
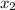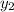`y_(2)`) = (-2.6810m, 2.2498m)

=> distance =
`\sqrt{(-2.6810 - 2.8191)^(2) + (2.2498 - 1.0260)^(2) }`

=> distance =
`\sqrt{(-5.5001)^(2) + (1.2238)^(2) }`

=> distance =
`√(30.2511+1.4977)`

=> distance =
`√(31.7488)`

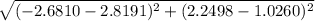
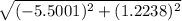
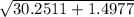
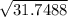
=> distance = 5.6346m

Answer 2

a)(2.82, 1.03) and (-2.68, 2.25)

b) 5.63 m

Step-by-step explanation:

a) The Cartesian coordinates of point (3.00 m, 20.0°) is

(3cos20.0°, 3sin20.0°) = (2.82, 1.03) m

The Cartesian coordinates of point (3.5 m, 140.0°) is

(3.5cos140.0°, 3.5sin140.0°) = (-2.68, 2.25) m

b) The distance between them

`d = √((2.82 - (-2.68))^2 + (1.03 - 2.25)^2) = √(5.5^2 + 1.22^2) = 5.63m`