Question

Suppose you would like to determine if the mean score for the first round of a golf tournament event is significantly different than the mean score for the fourth and final round. Does the pressure of playing in the final round cause scores to go up? Or does the increased player concentration cause scores to come down?

Answer 1

a. 0.10 < P < 0.20

b. -1.05

c. 1.2821

Step-by-step explanation:

The data represents the scores in the 1st and 4th rounds. The significance level is
`\alpha = 0.10`

• Hypotheses

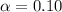
The null hypothesis H₀ = μ
`_(d)`

This means that there is no difference between the population mean score of the first round and the fourth round.

Alternative hypothesis:

`H_(a) :\\mu _(d) \\eq 0`

This means that there is a difference between the population score pf the 1st round and 4th round.

Testing

The testing method is as follows:

`t= (d -\mu _(d) )/((sd)/(√(n) ) )`

This can be solved using excel to give: 0.10 < P < 0.20

For part b) the main margin for error is 90 % confidence level. This means that there is no significant difference, hence - 1.05

For part c) the confidence interval from the tables is 1.2821. This means that the confidence interval can be used to rest the hypothesis.