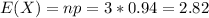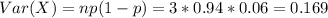Question

An optical inspection system is used to distinguish among different part types. The probability of a correct classification of any part is 0.94. Suppose that three parts are inspected and that the classifications are independent. Let the random variable X denote the number of parts that are correctly classified. Determine the mean and variance of X. Round your answers to three decimal places (e.g. 98.765).

Answer 1

Mean: 2.82

Variance: 0.169

Explanation:

For each part inspected there are only two possible outcomes. Either it is correctly classified, or it is not. So we use the binomal probability distribution to solve this problem.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

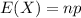
The variance of the binomial distribution is:

`Var(X) = np(1-p)`

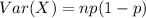
The probability of a correct classification of any part is 0.94.

This means that
`p = 0.94`

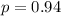
Three parts are inspected

This means that
`n = 3`

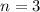
Determine the mean and variance of X.

`E(X) = np = 3*0.94 = 2.82`

`Var(X) = np(1-p) = 3*0.94*0.06 = 0.169`