Answer:
Explanation:
given that U, V are two vectors in R^n
These two vectors can be written as a linear combination of 3 vectors
w1, w2, and w3
To prove that U+V also can be written as a linear combination of these three vectors.
Since U is a linear combination we can write for not all a,b, c equal to 0
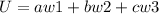
Similarly for d,e,f not all equal to 0
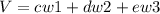
Adding these we have
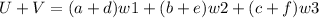
Here all a+d, b+e or c+f cannot be simultaneously 0.
So we get U+V can be written as a linear combination of w1, w2 w3 as follows:
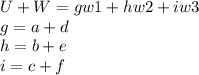
Proved