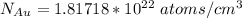Question

Gold forms a substitutional solid solution with silver. Compute the number of gold atoms per cubic centimeter for a silver-gold alloy that contains 45 wt% Au and 55 wt% Ag. The densities of pure gold and silver are 19.32 and 10.49 g/cm3, respectively. The atomic weight of Au is 196.97 g/mol.

Answer 1

The Number of gold atoms are =
`N_(Au)=1.81718*10^(22)\ atoms/cm^3`

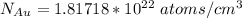
Step-by-step explanation:

The formula we are going to use is:

`N_(Au)=\frac{N_A*C_(Au)}{{(C_(Au)A_(Au) )/(\rho_(Au))}+(A_(Au))/(\rho_(Ag))(100-C_(Au))}`

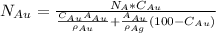
Where:

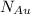`N_(Au)` are number of gold atoms.

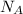`N_A` is Avogadro Number.

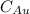`C_(Au)` is the amount of gold.

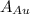`A_(Au)` is the atomic weight of gold.

`\rho_(Au)` is the density of gold.

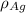`\rho_(Ag)` is the density of silver.

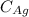`C_(Ag)` is the amount of silver.

`N_(Au)=(6.023*10^(23)*45\%wt)/((45\%wt*196.97)/(19.32)+(196.97)/(10.49)(100-45\%wt))\\ N_(Au)=1.81718*10^(22)\ atoms/cm^3`

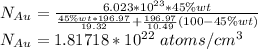
The Number of gold atoms are =
`N_(Au)=1.81718*10^(22)\ atoms/cm^3`