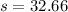Answer:
32.66 units
Explanation:
We are given that
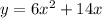
Point A=(-2,-4) and point B=(1,20)
Differentiate w.r. t x
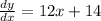
We know that length of curve
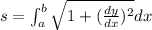
We have a=-2 and b=1
Using the formula
Length of curve=
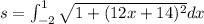
Using substitution method
Substitute t=12x+14
Differentiate w.r t. x
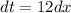
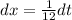
Length of curve=
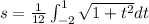
We know that
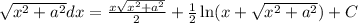
By using the formula
Length of curve=
![s=(1)/(12)[(t)/(2)√(1+t^2)+(1)/(2)ln(t+√(1+t^2))]^(1)_(-2)](https://img.qammunity.org/2021/formulas/mathematics/college/lyf389fc20tbf4x8yjjq6m4hud7gw0r16m.png)
Length of curve=
![s=(1)/(12)[(12x+14)/(2)√(1+(12x+14)^2)+(1)/(2)ln(12x+14+√(1+(12x+14)^2))]^(1)_(-2)](https://img.qammunity.org/2021/formulas/mathematics/college/kn46z0vi0d24p7lw7r86e4him2tlgj1dfr.png)
Length of curve=
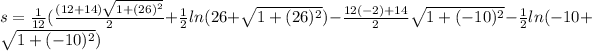
Length of curve=
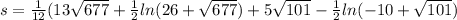
Length of curve=