Question

Arandom sample of n1 =12 students majoring in accounting in a college of business has a mean grade-point average of 2.70 (where A = 4.0) with a sample standard deviation of 0.40. For the students majoring in computer information systems, a random sample of n2 = 10 students has a mean grade-point average of 2.90 with a standard deviation of 0.30. The grade-point values are assumed to be normally distributed. Test the null hypothesis that the mean-grade point average for the two categories of students is not different, using the 5 percent level of significance.

Answer 1

We accept the null hypothesis that the mean gpa's are equal, with the 5 percent level of significance.

Explanation:

We have these following hypothesis:

Null

Equal means

So

`\mu_(1) = \mu_(2)`

Alternative

Different means

So

`\mu_(1) \\eq \mu_(2)`

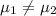
Our test statistic is:

`\frac{\overline{Y_(1)} - \overline{Y_(2)}}{\sqrt{(s_(1)^(2))/(N_(1)) + (s_(2)^(2))/(N_(2))}}`

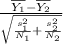
In which
`\overline{Y_(1)}, \overline{Y_(2)}` are the sample means,
`N_(1), N_(2)` are the sample sizes and
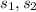`s_(1), s_(2)` are the standard deviations of the sample.

In this problem, we have that:

`\overline{Y_(1)} = 2.7, s_(1) = 0.4, N_(1) = 12, \overline{Y_(2)} = 2.9, s_(2) = 0.3, N_(2) = 10`

So

`T = \frac{2.7 - 2.9}{\sqrt{\frac{0.4}^(2){12} + \frac{0.3}^(2){10}}} = -1.3383`

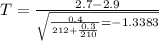
What to do with the null hypothesis?

We will reject the null hypothesis, that is, that the means are equal, with a significante level of
`\alpha` if

`|T| > t_{1-(\alpha)/(2),v}`

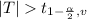
In which v is the number of degrees of freedom, given by

`v = (((s_(1)^(2))/(N_(1)) + (s_(2)^(2))/(N_(2)))^(2))/(((s_(1)^(2))/(N_(1)))/(N_(1)-1) + ((s_(2)^(2))/(N_(2)))/(N_(2) - 1))`

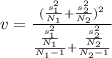
Applying the formula in this problem, we have that:

`v = 20`

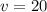
So, applying t at the t-table at a level of 0.975, with 20 degrees of freedom, we find that

`t = 2.086`

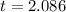
We have that

`|T| = 1.3383`

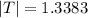
Which is lesser than t.

So we accept the null hypothesis that the mean gpa's are equal, with the 5 percent level of significance.