Answer:
See proof
Explanation:
Statement Reason
1.
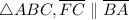 and
and
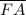 bisects
bisects
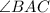 - Given
- Given
2.
 - Definition of angle bisector
- Definition of angle bisector
3.
 - Alternate interior angles theorem
- Alternate interior angles theorem
4.
 - Substitution property
- Substitution property
5.
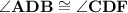 - Vertical angles are congruent
- Vertical angles are congruent
6.
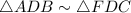 - AA Similarity postulate
- AA Similarity postulate
7.
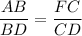 - Definition of similar triangles
- Definition of similar triangles
8.
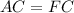 - Converse of base angles theorem
- Converse of base angles theorem
9.
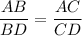 - Substitution property
- Substitution property