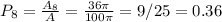Question

Suppose you throw a dart at a circular target of radius 10 inches. Assuming that you hit the target and that the coordinates of the outcomes are chosen at random, find the probability that the dart falls (a) within 2 inches of the center. (b) within 2 inches of the rim.

Answer 1

a)0.04

b)0.36

Step-by-step explanation:

The probability of you randomly hitting the dart of a portion of the target would be the ratio of the area of the portion over the total area of the target.

Knowing that radius r = 10 in, the total area of the target is

`A = \pi r^2 = \pi 10^2 = 100 \pi in^2`

a)The area of the portion that is 2 inches from the center

`A_2 = \pi 2^2 = 4 \pi`

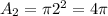
The chance of the dart hitting within 2 inches of the center is

`P_2 = (A_2)/(A) = (4\pi)/(100\pi) = 1/25 = 0.04`

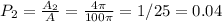
b) the area of the portion that is 2 inches from the rim is the total area of the target subtracted by the area of the 8 in radius circle

`A_8 = A - \pi 8^2 = 100 \pi - 64 \pi = 36 \pi`

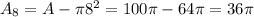
The chance of the dart hitting within 2 inches from the rim is

`P_8 = (A_8)/(A) = (36\pi)/(100\pi) = 9/25 = 0.36`