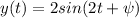Question

Help asap!!!!! Picture below

Answer 1

Maximum value :

It is the peak value of the sine wave from the origin along the positive y axis

In the given sine wave the Maximum value is 1

Minimum value :

It is the peak value of the sine wave from the origin along the negative y axis

In the given sine wave the Maximum value is -3

Midline :

It is the horizontal line that passes exactly in the middle between the graph's maximum and minimum points.

Here in the given graph the mid line is y = -1

since the maximum and minimum points are 1 and -3 respectively

Amplitude:

The vertical distance between the mid-line and one of the extremum points.

From the graph , the amplitude is 2

Period:

The distance between two consecutive maximum points, or two consecutive minimum points (these distances must be equal).

In the graph the period is
`\pi`

Frequency:

Frequency is the number of cycles in a unit of time

Frequency =
`(1)/(period)`

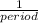
Frequency =
`(1)/(\pi)`

Equation of the graphed function:

The general equation of the sine wave is

`y(t) = Asin(\omega t + \psi)`

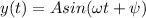
where

A is the amplitude

`\omega` is the angular frequency and is equal to
`2\pi f`

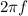
f is the frequency

t is the time

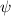`\psi` is the phase

Now substituting the values we gte

`y(t) = 2sin(2t +\psi)`