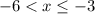Question

Solve the following inequality. 21<_-3(x - 4) < 30 A. 28<_x < 37 B. -3 <_ x < 6 C. -6 < x <_ -3 D. -10 < x <_ -3

Answer 1

Option C
`-6<x\leq -3`

Explanation:

we have

`21\leq -3(x-4)<30`

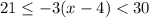
The compound inequality can be divided into two inequality

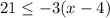`21\leq -3(x-4)` -----> inequality A

`-3(x-4)<30` ----> inequality B

Solve inequality A

`21\leq -3x+12`

`9\leq -3x`

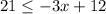
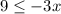
Divide by -3 both sides

when you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol

`-3\geq x`

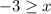
Rewrite

`x\leq -3`

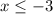
The solution of the inequality A is the interval (-∞,-3]

Solve the inequality B

`-3x+12<30`

`-3x<18`

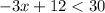
Divide by -3 both sides

when you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol

`x>-6`

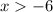
The solution of the inequality B is the interval [-6,∞)

The solution of the compound inequality is

[-6,∞) ∩ (-∞,-3]=(-6,-3]

`-6<x\leq -3`