Question

A wall has inner and outer surface temperatures of 25◦C and 8◦C, respectively. The interior and exterior air temperatures are 35◦C and −3 ◦C, respectively. The inner and outer convection heat transfer coefficients are 6 W/m2 ·K and 10 W/m2 ·K, respectively. Calculate and state the direction of the heat flux between (a) the interior air and the wall, and (b) the exterior air and the wall. (c) Is the wall under steady-state conditions? State your reasoning

Answer 1

a)
`(\dot Q)/(A) =60\ W.m^(-2)`

b)
`(\dot Q)/(A) =110\ W.m^(-2)`

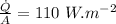
c) The wall may not be under steady because the two surfaces of the wall are exposed to the air at different temperatures and they have different convective coefficient.

Step-by-step explanation:

Given:

• temperature of the inner surface of the wall,
  `T_i=25^(\circ)C`

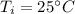
• temperature of the outer surface of the wall,
  `T_o=8^(\circ)C`

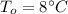
• temperature of the air outside,
  `T_(ao)=-3^(\circ)C`

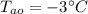
• temperature of the air inside,
  `T_(ai)=35^(\circ)C`

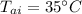
• coefficient of heat convection on outside,
  `h_o=10\ W.m^(-2).K^(-1)`

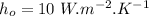
• coefficient of heat convection on inside,
  `h_i=6\ W.m^(-2).K^(-1)`

a)

The heat flux between the interior air and the wall:

The convective heat transfer rate is given as,

`Q=h_i.A.\Delta T`

`\Rightarrow (\dot Q)/(A) =h_i* (T_(ai)-T_i)`

`(\dot Q)/(A) =6* (35-25)`

`(\dot Q)/(A) =60\ W.m^(-2)`

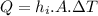
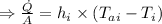
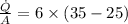
b)

The heat flux between the exterior air and the wall:

`\Rightarrow (\dot Q)/(A) =h_o* (T_(ao)-T_i)`

`(\dot Q)/(A)=10* (8-(-3))`

`(\dot Q)/(A) =110\ W.m^(-2)`

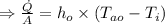
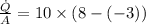
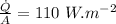
c)

The wall may not be under steady because the two surfaces of the wall are exposed to the air at different temperatures and they have different convective coefficient.