Question

At 298 K, the osmotic pressure of a glucose solution (C6H12O6 (aq)) is 12.1 atm. Calculate the freezing point of the solution. The density of the solution is 1.034 g/mL.

Answer 1

To calculate the freezing point of a glucose solution with known osmotic pressure and density, one must first find the molarity from the osmotic pressure, then convert it to molality considering the density, and finally apply the freezing point depression equation using the cryoscopic constant.

Step-by-step explanation:

The question asks to calculate the freezing point of a glucose solution with an osmotic pressure of 12.1 atm at 298 K and a density of 1.034 g/mL. To find the freezing point depression, ΔTf, we can use the formula ΔTf = i * Kf * m, where i is the van't Hoff factor (which is 1 for glucose as it does not ionize), Kf is the cryoscopic constant for the solvent (in this case water, which is 1.86 °C·kg/mol), and m is the molality of the solution.

First, we need to determine the molarity (M) of the glucose solution using the formula for osmotic pressure Π = MRT, where R is the ideal gas constant (0.0821 L·atm/K·mol), T is the temperature in Kelvin, and Π is the osmotic pressure. Given that the osmotic pressure is 12.1 atm and the temperature is 298 K, we can solve for M. After finding the molarity, we convert it to molality (m) using the density of the solution. Finally, we use the freezing point depression equation to find the freezing point of the solution.

Answer 2

Answer: The freezing point of solution is -0.974°C

Step-by-step explanation:

• To calculate the concentration of solute, we use the equation for osmotic pressure, which is:

`\pi=iMRT`

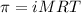
where,

`\pi` = osmotic pressure of the solution = 12.1 atm

i = Van't hoff factor = 1 (for non-electrolytes)

M = molarity of solute = ?

R = Gas constant =
`0.0821\text{ L atm }mol^(-1)K^(-1)`

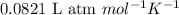
T = temperature of the solution = 298 K

Putting values in above equation, we get:

`12.1atm=1* M* 0.0821\text{ L.atm }mol^(-1)K^(-1)* 298K\\\\M=(12.1)/(1* 0.0821* 298)=0.495M`

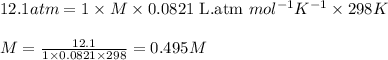
This means that 0.495 moles of glucose is present in 1 L or 1000 mL of solution

• To calculate the mass of solution, we use the equation:

`\text{Density of substance}=\frac{\text{Mass of substance}}{\text{Volume of substance}}`

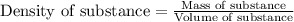
Density of solution = 1.034 g/mL

Volume of solution = 1000 mL

Putting values in above equation, we get:

`1.034g/mL=\frac{\text{Mass of solution}}{1000mL}\\\\\text{Mass of solution}=(1.034g/mL* 1000mL)=1034g`

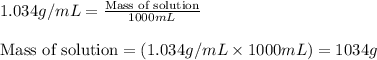
• To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

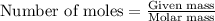
Moles of glucose = 0.495 moles

Molar mass of glucose = 180.16 g/mol

Putting values in above equation, we get:

`0.495mol=\frac{\text{Mass of glucose}}{180.16g/mol}\\\\\text{Mass of glucose}=(0.495mol* 180.16g/mol)=89.18g`

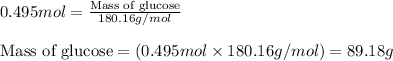
Depression in freezing point is defined as the difference in the freezing point of pure solution and freezing point of solution.

• The equation used to calculate depression in freezing point follows:

`\Delta T_f=\text{Freezing point of pure solution}-\text{Freezing point of solution}`

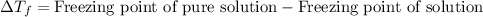
To calculate the depression in freezing point, we use the equation:

`\Delta T_f=iK_fm`

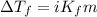
Or,

`\text{Freezing point of pure solution}-\text{Freezing point of solution}=i* K_f* \frac{m_(solute)* 1000}{M_(solute)* W_(solvent)\text{ (in grams)}}`

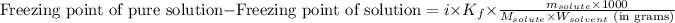
where,

Freezing point of pure solution = 0°C

i = Vant hoff factor = 1 (For non-electrolytes)

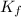`K_f` = molal freezing point elevation constant = 1.86°C/m

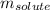`m_(solute)` = Given mass of solute (glucose) = 89.18 g

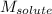`M_(solute)` = Molar mass of solute (glucose) = 180.16 g/mol

`W_(solvent)` = Mass of solvent (water) = [1034 - 89.18] g = 944.82 g

Putting values in above equation, we get:

`0-\text{Freezing point of solution}=1* 1.86^oC/m* (89.18* 1000)/(180.16g/mol* 944.82)\\\\\text{Freezing point of solution}=-0.974^oC`

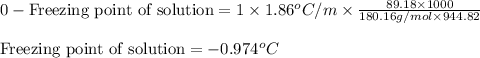
Hence, the freezing point of solution is -0.974°C