Question

g What is the probability of being dealt exactly three of a kind (like three kings or three 7’s, etc.) in a five card hand from a deck of 52 cards?

Answer 1

Answer: 0.02257

Explanation:

Given : Total cards in a deck = 52

Number of ways to select any 5 cards :
`^(52)C_5`

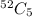
Since , there are total 13 kinds of card (includes Numbers from 2 to 9 and Ace , king, queen and jack).

Of each kind , there are 4 cards.

Number of ways to select three cards in a five card hand of a single kind :
`^(4)C_3*^(48)C_2`

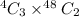
Number of ways to select three cards in a five card hand of a exactly three of a kind :
`13*^(4)C_3*^(48)C_2`

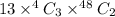
Now , the required probability =
`(13*^(4)C_3*^(48)C_2)/(^(52)C_5)`

`=(13*4*(48!)/(2!46!))/((52!)/(5!47!))\\\\\\=(58656)/(2598960)`

`=0.022569027611\approx0.02257`

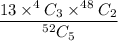
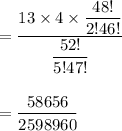
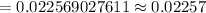
∴ The probability of being dealt exactly three of a kind (like three kings or three 7’s, etc.) in a five card hand from a deck of 52 cards= 0.02257