Answer: 0.02257
Explanation:
Given : Total cards in a deck = 52
Number of ways to select any 5 cards :
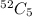
Since , there are total 13 kinds of card (includes Numbers from 2 to 9 and Ace , king, queen and jack).
Of each kind , there are 4 cards.
Number of ways to select three cards in a five card hand of a single kind :
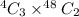
Number of ways to select three cards in a five card hand of a exactly three of a kind :
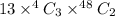
Now , the required probability =
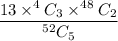
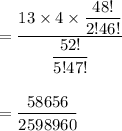
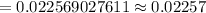
∴ The probability of being dealt exactly three of a kind (like three kings or three 7’s, etc.) in a five card hand from a deck of 52 cards= 0.02257