Question

A manufacturer of chocolate chips would like to know whether its bag filling machine works correctly at the 435.0435.0 gram setting. It is believed that the machine is underfilling the bags. A 4646 bag sample had a mean of 429.0429.0 grams. A level of significance of 0.050.05 will be used. Determine the decision rule. Assume the standard deviation is known to be 24.024.0.

Answer 1

The machine is underfilling the bags.

Explanation:

We are given the following in the question:

Population mean, μ = 435.0 grams

Sample mean,
`\bar{x}` = 429.0 grams

Sample size, n = 46

Alpha, α = 0.05

Population standard deviation, σ = 24.0 grams

First, we design the null and the alternate hypothesis

`H_(0): \mu = 435.0\text{ grams}\\H_A: \mu < 435.0\text{ grams}`

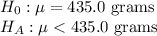
We use one-tailed z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

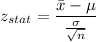
Putting all the values, we have

`z_(stat) = \displaystyle(429.0 - 435.0)/((24.0)/(√(46)) ) = -1.695`

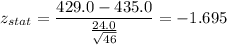
Now,
`z_(critical) \text{ at 0.05 level of significance } = -1.64`

Decision Rule:

If the calculated z statistic is less than the critical value of z, we fail to accept the null hypothesis and reject it.

Since,

`z_(stat) < z_(critical)`

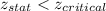
We reject the null hypothesis and accept the alternate hypothesis. Thus, the machine is underfilling the bags.