Question

6. A 1500 MΩ resistor is placed across the terminals of a battery, and a terminal voltage of 2.50 V is measured. When this resistor is replaced with a 5.00 Ω resistor, the terminal voltage decreases to 1.75 V. Find the terminal voltage when a 7.00 Ω resistor is used. (1 point)

Answer 1

The terminal voltage is 1.916 V.

Step-by-step explanation:

Given that,

Resistance = 1500 MΩ

Voltage V= 2.50 V

Decrease voltage V' = 1.75 V

Here, The resistance is very high so the current will be zero in the terminal.

So, the potential difference will be equal to the emf.

`V=2.50 = emf`

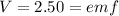
Let the internal resistance is r ohm.

We need to calculate the potential difference across internal resistance

Using formula of for potential difference

`V_(r)=V-V'`

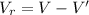
Put the value into the formula

`V_(r)=2.50-1.75`

`V_(r)=0.75\ V`

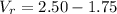
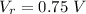
We need to calculate the circuit current

Using formula of current

`i=(V)/(R)`

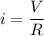
Put the value into the formula

`i=(1.75)/(5.00)`

`i=0.35\ A`

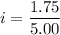
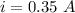
We need to calculate the internal resistance

Using formula of internal resistance

`r=(V_(r))/(i)`

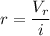
Put the value into thew formula

`r=(0.75)/(0.35)`

`r=2.14\ ohm`

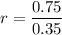
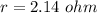
We need to calculate the current

Using formula of current

`i=(emf)/(r+R)`

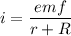
Put the value into the formula

`i=(2.50)/(2.14+7.00)`

`i=0.273\ A`

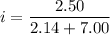
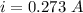
We need to calculate the potential difference

Using formula of voltage

`V_(r)=ir`

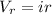
Put the value into the formula

`V_(r)=0.273*2.14`

`V_(r)=0.584\ V`

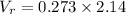
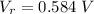
We need to calculate the terminal voltage

Using formula of terminal voltage

`\text{terminal voltage}=emf-V_(r)`

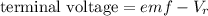
Put the value into the formula

`\text{terminal voltage}=2.50-0.584`

`\text{terminal voltage}=1.916\ V`

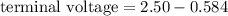
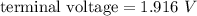
Hence, The terminal voltage is 1.916 V.