1 Answer

Avshalom · Answer 1 · 2021-07-12T03:14:07+0000

Option B:
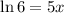$\ln 6=5 x$ is the correct answer.

Step-by-step explanation:

The exponential equation is
e^(5 x)=6

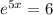
If
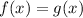f(x)=g(x) , then
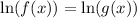
$\ln (f(x))=\ln (g(x))$

Thus, the equation becomes

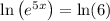
$\ln \left(e^(5 x)\right)=\ln (6)$

Applying log rule,
$\log _(a)\left(x^(b)\right)=b \cdot \log _(a)(x)$ and thus the equation becomes

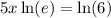
$5 x \ln (e)=\ln (6)$

Since, we know that,
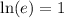$\ln (e)=1$ , using this we get,

$5 x=\ln (6)$

Hence, the logarithmic equation which is equivalent to the exponential equation
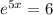e^(5 x)=6 is
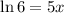
$\ln 6=5 x$

Thus, Option B is the correct answer.

Please log in or register to add a comment.