Question

Find the vertex of the quadratic function given below.

f(t) = (x – 4)(x + 2)
A.
B.
(1,-9)
(-4,2)
C. (-1,9)
OD. (4,-2)
Reset
Next

Answer 1

The answer is (1, -9) which is the vertex otherwise known as the minimum. It is where the graph comes to a curve.

Answer 2

One way to do it is to expand the quadratic, then complete the square to write it in vertex form:

`(x-4)(x+2)=x^2-2x-8=(x-1)^2-9`

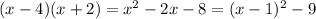
Then we get the vertex right away, (1, -9).

Alternatively, if you know about the parity/symmetry of parabolas, you know that the vertex lies on a line between its roots. In this case, we know
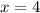`x=4` and
`x=-2` are the roots to this quadratic. The line
`x=1` falls in the middle of these two points (if you're unsure as to why, take the average of the roots: (4 - 2)/2 = 1). So we know the
`x`-coordinate of the vertex, and the
`y`-coordinate is
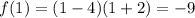`f(1)=(1-4)(1+2)=-9`, so we again get (1, -9).