Question

(a) Suppose you have 9 gold coins that look identical, but you also know one (and only one) of them is counterfeit. The counterfeit coin weighs slightly less than the others. You also have access to a balance scale to compare the weight of two sets of coins — i.e., it can tell you whether one set of coins is heavier, lighter, or equal in weight to another (and no other information). However, your access to this scale is very limited. Can you find the counterfeit coin using just two weighings? Prove your answer.

(b) Now consider a generalization of the same scenario described above. You now have 3^n coins, n ≥ 1, only one of which is counterfeit. You wish to find the counterfeit coin with just n weighings. Can you do it? Prove your answer

Answer 1

Explanation:

You can split the coins into 3 groups, each of them has 3 coins. Weigh group 1 vs group 2, if one is lighter, that group has the fake coin. If both groups weigh the same, then group 3 has the fake coin.

Continue to split the group that has the fake coin into 3 groups, each group has 1 coin. Now apply the same procedure and we can identify the fake coin.

Total of scale usage is 2

b) if you have
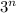`3^n` coins then you can apply the same approach and find the fake coin with just n steps. By splitting up to 3 groups each step, after each step you should be able to narrow down your suspected coin by 3 times.

Step 1: you narrow down to group of
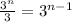`(3^n)/(3) = 3^(n-1)` coins

Step 2: you narrow down to group of
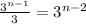`(3^(n-1))/(3) = 3^(n-2)` coins

Step 3: you narrow down to group of
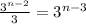`(3^(n-2))/(3) = 3^(n-3)` coins

...

Step n: Step 1: you narrow down to group of
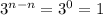`3^(n-n) = 3^0 = 1`coin