Question

Help me please, i can't solve it

Answer 1

The length of BC is 2.30

Step-by-step explanation:

It is given that AB = 3 and ∠A = 50°

To find the length of BC, let us use the sine formula.

The formula is given by

`\sin \theta=(o p p)/(h y p)`

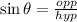
where
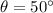`\theta=50^(\circ)`, opp = BC and hyp = AB

Thus, substituting these in the formula, we get,

`\sin 50=(B C)/(A B)`

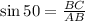
From the diagram, the value of AB is 3.

Substituting the value and simplifying the expression, we have,

`0.7660=(B C)/(3)`

Multiplying both sides by 3, we get,

`2.298={B C}`

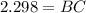
Rounding the answer to the nearest hundredth, we have,

`BC=2.30`

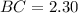
Thus, the length of BC is 2.30