Question

Which expression is equivalent to StartFraction (3 m Superscript negative 2 Baseline n) Superscript negative 3 Baseline Over 6 m n Superscript negative 2 Baseline EndFraction? Assume m not-equals 0, n not-equals 0.

StartFraction m Superscript 5 Baseline Over 162 n EndFraction
StartFraction 1 Over 2 m cubed n EndFraction
StartFraction 8 m Superscript 9 Baseline Over n Superscript 9 Baseline EndFraction
StartFraction 4 m Superscript 8 Baseline Over 3 n cubed EndFraction

Answer 1

A.) m5/162n

Step-by-step explanation:

Answer 2

Option a:
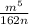`(m^(5) )/(162n)` is the equivalent expression.

Step-by-step explanation:

The expression is
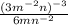`((3m^(-2) n)^(-3))/(6mn^(-2) )` where
`m\\eq 0, n\\eq 0`

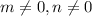
Let us simplify the expression, to determine which expression is equivalent from the four options.

Multiplying the powers, we get,

`(3^(-3)m^(6) n^(-3))/(6mn^(-2) )`

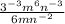
Cancelling the like terms, we have,

`(3^(-3)m^(5) n^(-1))/(6 )`

This equation can also be written as,

`(m^(5))/(3^(3)6 n^(1) )`

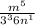
Multiplying the terms in denominator, we have,

`(m^(5) )/(162n)`

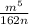
Thus, the expression which is equivalent to
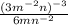`((3m^(-2) n)^(-3))/(6mn^(-2) )` is
`(m^(5) )/(162n)`

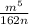
Hence, Option a is the correct answer.